好的，这是您提供的文本，其中相关的物理化学名词已加粗，并保持了原有的格式。

十二烷基硫酸钠（SDS）胶束化的热力学：一项本科生实验室实验

Juan P. Marcolongo 和 Martín Mirenda*<br>布宜诺斯艾利斯大学精确与自然科学学院无机、分析与物理化学系，1428，布宜诺斯艾利斯，阿根廷

(S) 辅助信息

0 摘要

本文介绍了一项本科生实验室实验，该实验可对十二烷基硫酸钠（SDS）在水溶液中形成胶束进行热力学表征。通过电导法在不同温度下测定临界胶束浓度（CMC）和胶束电离度（ α\alpha ）。在简化的闭合缔合模型框架内，该模型假设游离表面活性剂****单体与单分散胶束之间存在平衡，利用CMC、 α\alpha 及其温度依赖性计算胶束化过程的摩尔标准自由能（ Δmic Gˉ\Delta_{\text {mic }} \bar{G} ）、焓（ Δmic Hˉ∘\Delta_{\text {mic }} \bar{H}^{\circ} ）和熵（ Δmic Sˉ∘\Delta_{\text {mic }} \bar{S}^{\circ} ）。在此基础上，还对结果提出了基于表面活性剂分子水合现象的物理化学讨论。

关键词：高年级本科生，物理化学，实验室教学，动手学习/操作，水溶液化学，电导率，胶束，有机硫化合物，热力学

1 引言

表面活性剂（surface active agent）是两亲性化合物，包含一个疏水“尾部”和一个极性（离子或非离子）“头部”。它们广泛存在于日常生活中使用的众多商业产品中，如洗涤剂、洗发水和油。尽管胶束态日益重要，但在大多数普通或实验物理化学教科书中通常被忽视。由于这些系统对化学家来说具有明显的专业相关性，因此将其研究纳入本科教育课程是一个重要领域。

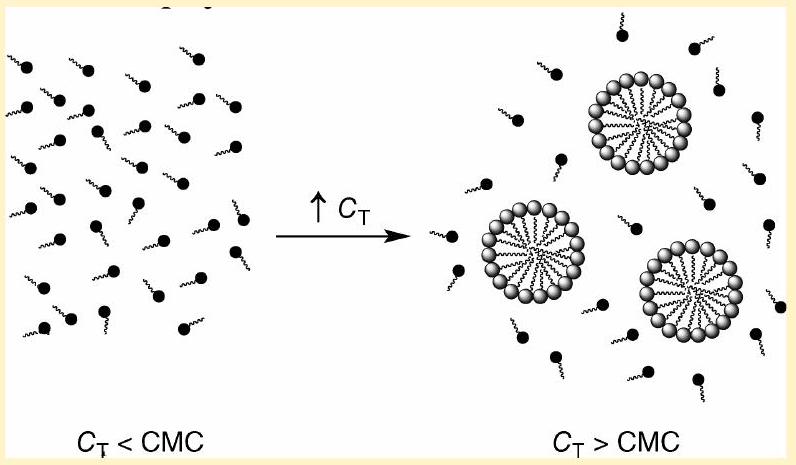
众所周知，当表面活性剂浓度超过一个临界值（通常称为临界胶束浓度，CMC）时，溶液中的表面活性剂分子会自发地排列成自组织的胶束结构。本刊已提出多项实验，旨在让本科生熟悉胶束系统¹˒² 以及测定CMC值的实验技术³⁻⁷。然而，这些文章并未在本科水平上处理这些系统的热力学解释。

在宽浓度范围内进行的离子表面活性剂溶液的电导率测量可用于确定CMC和胶束电离度 α\alpha 。该方法依赖于溶液中游离表面活性剂分子的电导率与胶束排列中分子相关联时的电导率之间的差异。尽管其应用广泛，但文献中存在不同的方法来描述观察到的电导率数据。一些作者认为构成胶束的表面活性剂****单体的电导率应与溶液中游离单体的电导率相同⁸⁻¹⁰，而另一些作者则认为该电导率应更方便地以斯托克斯定律表示¹¹。然而，通过这两种方法获得的CMC是相同的，而 α\alpha 则有明显的差异。

在不同温度下获得的CMC值可用于胶束形成的热力学表征。这需要以显式形式评估CMC的温度依赖性，这可以通过使用不同代数表达式拟合实验数据来获得。Kim和Lim¹⁶建议使用 ln⁡CMC=A+BT+C/T\ln \mathrm{CMC}=A+B T+C/T 形式的函数，而非广泛使用的二阶¹²˒¹⁴˒¹⁵ 和三阶多项式表达式⁹，理由是前者没有理论基础。通常，与胶束系统相关的热力学量计算不考虑 α\alpha 对温度的依赖性¹⁰˒¹⁷，这导致相关热力学信息存在不可忽略的差异¹⁸。

由于胶束系统文献中存在多种方法，以及需要在本科课程中引入新的实验室实验，本文提出了一项简单、可靠且经济的实验，用于提取离子表面活性剂在水溶液中胶束化过程相关的热力学信息。当前的实验室实验基于在不同温度下通过测量电导率来确定十二烷基硫酸钠（SDS）的CMC。使用简单的“闭合缔合模型”，该实验涉及胶束化****热力学参数的计算及其基于表面活性剂分子水合现象等概念的物理解释。

2 闭合缔合模型

采用闭合缔合模型来分析实验数据。该模型假设溶液中游离表面活性剂分子与单分散胶束处于化学平衡状态，每个温度下胶束均由固定数量 nn 的表面活性剂分子组成。通常，胶束溶液并非单分散¹⁹˒²⁰；然而，文献中已表明²¹˒²²，这种偏差不会显著影响模型的有效性。为了描述SDS表面活性剂在无盐水溶液中的胶束化过程，提出了以下平衡：

n S−+(n−m)Na+⇌Kmic (SnNan−m)m−n \mathrm{~S}^{-}+(n-m) \mathrm{Na}^{+} \stackrel{K_{\text {mic }}}{\rightleftharpoons}\left(\mathrm{S}_{n} \mathrm{Na}_{n-m}\right)^{m-}

其中 S−\mathrm{S}^{-}和 Na+\mathrm{Na}^{+}分别代表十二烷基硫酸根阴离子和钠阳离子，胶束 (SnNan−m)m−\left(\mathrm{S}_{n} \mathrm{Na}_{n-m}\right)^{m-} 是带净电荷 −m-m 的部分，包含 nn 个SDS分子和 (n−m)(n-m) 个钠离子。相应的单体-胶束****平衡常数 KmicK_{\mathrm{mic}} 可表示为

Kmic=[(SnNan−m)m−][S−]n[Na+]n−m\begin{equation*} K_{\mathrm{mic}}=\frac{\left[\left(\mathrm{S}_{n} \mathrm{Na}_{n-m}\right)^{m-}\right]}{\left[\mathrm{S}^{-}\right]^{n}\left[\mathrm{Na}^{+}\right]^{n-m}} \tag{1} \end{equation*}

其中方括号表示摩尔浓度。通常，CMC足够低，因此离子活度系数可以安全地近似为1。

3 热力学计算

胶束形成的标准自由能 ΔmicGˉ∘\Delta_{\mathrm{mic}} \bar{G}^{\circ} 可以用 KmicK_{\mathrm{mic}} 表示：

ΔmicGˉ∘=−RTln⁡Kmic\begin{equation*} \Delta_{\mathrm{mic}} \bar{G}^{\circ}=-R T \ln K_{\mathrm{mic}} \tag{2} \end{equation*}

结合方程1和2并除以 nn，我们得到

ΔmicG∘n=ΔmicGˉ∘=−RTnln⁡[(SnNan−m)m−]+RTln⁡[ S−]+(1−α)RTln⁡[Na+]\begin{align*} \frac{\Delta_{\mathrm{mic}} G^{\circ}}{n}=\Delta_{\mathrm{mic}} \bar{G}^{\circ}= & -\frac{R T}{n} \ln \left[\left(S_{n} \mathrm{Na}_{n-m}\right)^{m-}\right]+R T \ln \left[\mathrm{~S}^{-}\right] \\ & +(1-\alpha) R T \ln \left[\mathrm{Na}^{+}\right] \tag{3} \end{align*}

其中 α=m/n\alpha=m/n 是胶束电离度。考虑到SDS胶束通常包含大量表面活性剂分子（ n>50n>50 ），方程3右侧的第一项相对于其他两项可以忽略不计。此外，当表面活性剂浓度接近CMC时， [S−]≈[Na+]≈CMC[\mathrm{S}^{-}] \approx [\mathrm{Na}^{+}] \approx \mathrm{CMC}。在这种情况下，方程3可以重写为

ΔmicGˉ∘≈RT(2−α)ln⁡CMC\begin{equation*} \Delta_{\mathrm{mic}} \bar{G}^{\circ} \approx R T(2-\alpha) \ln \mathrm{CMC} \tag{4} \end{equation*}

上述表达式可以插入经典的吉布斯-赫姆霍兹方程

∂(ΔG/T)∂T=−ΔHT2\frac{\partial(\Delta G / T)}{\partial T}=\frac{-\Delta H}{T^{2}}

得到胶束形成的摩尔标准焓 ΔmicHˉ∘\Delta_{\mathrm{mic}} \bar{H}^{\circ} 的以下表达式，

ΔmicHˉ∘≈−RT2[(2−α)(∂ln⁡CMC∂T)−(∂α∂T)ln⁡CMC]\begin{equation*} \Delta_{\mathrm{mic}} \bar{H}^{\circ} \approx-R T^{2}\left[(2-\alpha)\left(\frac{\partial \ln \mathrm{CMC}}{\partial T}\right)-\left(\frac{\partial \alpha}{\partial T}\right) \ln \mathrm{CMC}\right] \tag{5} \end{equation*}

最后，胶束形成的摩尔标准熵 ΔmicSˉ∘\Delta_{\mathrm{mic}} \bar{S}^{\circ} 可以使用以下公式计算

ΔmicGˉ∘=ΔmicHˉ∘−TΔmicSˉ∘\begin{equation*} \Delta_{\mathrm{mic}} \bar{G}^{\circ}=\Delta_{\mathrm{mic}} \bar{H}^{\circ}-T \Delta_{\mathrm{mic}} \bar{S}^{\circ} \tag{6} \end{equation*}

4 通过电导率测量确定CMC和 α\alpha

胶束形成的热力学计算所需的CMC和 α\alpha 值可以通过电导法获得。Bachofer previously在《本刊》中报道了离子表面活性剂的电导率测量⁴。描述离子表面活性剂溶液在CMC以下或以上的电导率的数学表达式是不同的。在CMC以下，SDS分子被认为是完全解离的1:1强电解质。在这种情况下，假设离子摩尔电导率与浓度无关，表面活性剂溶液的电导率 κ\kappa 可以计算为

κ=(λS−+λNa+)CT=p1CT\begin{equation*} \kappa=\left(\lambda^{S^{-}}+\lambda^{\mathrm{Na}^{+}}\right) C_{\mathrm{T}}=p_{1} C_{\mathrm{T}} \tag{7} \end{equation*}

其中 λS−\lambda^{\mathrm{S}-} 和 λNa+\lambda^{\mathrm{Na}+} 分别是十二烷基硫酸根阴离子和 Na+\mathrm{Na}^{+}的离子摩尔电导率（以 mS M−1^{-1} cm−1^{-1} 表示）， CTC_{\mathrm{T}} 是总摩尔表面活性剂浓度， p1p_1 代表在CMC以下 κ\kappa 对 CTC_{\mathrm{T}} 作线性拟合的斜率。

在CMC以上，游离SDS分子与胶束结构共存，胶束结构被认为是弱电解质。SDS浓度的增加导致胶束浓度的增加，而游离表面活性剂浓度在CMC值附近实际上保持不变。在这种情况下，SDS溶液的电导率可以表示为

κ=CMC(λS−+λNa+)+CT−CMCnλmic+(CT−CMC)αλNa+\begin{gather*} \kappa=\mathrm{CMC}\left(\lambda^{\mathrm{S}^{-}}+\lambda^{\mathrm{Na}^{+}}\right)+\frac{C_{\mathrm{T}}-\mathrm{CMC}}{n} \lambda^{\mathrm{mic}} \\ +\left(C_{\mathrm{T}}-\mathrm{CMC}\right) \alpha \lambda^{\mathrm{Na}^{+}} \tag{8} \end{gather*}

其中 λmic\lambda^{\mathrm{mic}} 是胶束的离子电导率，(CT−CMC)/n(C_{\mathrm{T}}-\mathrm{CMC})/n 是胶束的摩尔浓度。原则上， λmic\lambda^{\mathrm{mic}} 的值是未知的，但可以使用两种不同的方法进行估计：（i）认为 λmic=nαλS−\lambda^{\mathrm{mic}}=n\alpha\lambda^{\mathrm{S}-}，或（ii）采用斯托克斯定律，该定律规定球形离子的电导率与电荷的平方除以离子半径成正比。使用后一种方法，获得的热力学量与文献报道的 ΔmicHˉ∘\Delta_{\mathrm{mic}} \bar{H}^{\circ} 值吻合良好。

假设胶束半径与 n1/3n^{1/3} 成比例¹¹， λmic\lambda^{\mathrm{mic}} 可以近似为

λmic≈m2n1/3λS−\begin{equation*} \lambda^{\mathrm{mic}} \approx \frac{m^{2}}{n^{1/3}} \lambda^{\mathrm{S}^{-}} \tag{9} \end{equation*}

在斯托克斯定律近似的范畴内， λmic\lambda^{\mathrm{mic}} 的值可以从 λS−\lambda^{\mathrm{S}-} 估计，即单电荷（ m=−1m=-1 ）SDS单体（ n=1n=1 ）的电导率。方程8可以重新排列得到

κ−CMC(λS−+λNa+)CT−CMC=1nλmic+αλNa+\begin{equation*} \frac{\kappa-\mathrm{CMC}\left(\lambda^{\mathrm{S}^{-}}+\lambda^{\mathrm{Na}^{+}}\right)}{C_{\mathrm{T}}-\mathrm{CMC}}=\frac{1}{n} \lambda^{\mathrm{mic}}+\alpha \lambda^{\mathrm{Na}^{+}} \tag{10} \end{equation*}

将方程7和9代入方程10并重新排列，得到以下表达式

κ−CMC(λS−+λNa+)CT−CMC=m2n4/3(p1−λNa+)+αλNa+\begin{equation*} \frac{\kappa-\mathrm{CMC}\left(\lambda^{\mathrm{S}^{-}}+\lambda^{\mathrm{Na}^{+}}\right)}{C_{\mathrm{T}}-\mathrm{CMC}}=\frac{m^{2}}{n^{4/3}}\left(p_{1}-\lambda^{\mathrm{Na}^{+}}\right)+\alpha \lambda^{\mathrm{Na}^{+}} \tag{11} \end{equation*}

方程11的左侧表示CMC以上 κ\kappa 对 CTC_{\mathrm{T}} 作线性拟合的斜率 p2p_2。考虑到 α=m/n\alpha=m/n 的定义，此方程可以改写为二次方程

n2/3(p1−λNa+)α2+λNa+α−p2=0\begin{equation*} n^{2/3}\left(p_{1}-\lambda^{\mathrm{Na}^{+}}\right) \alpha^{2}+\lambda^{\mathrm{Na}^{+}} \alpha-p_{2}=0 \tag{12} \end{equation*}

为了从方程12中评估 α\alpha ，需要额外的假设：（i）首先，允许 nn 随温度变化。Zana及其同事¹³报告的实验数据通过内插和外推法获得了 nn 值： n=72n=72 （ T=284 KT=284 \mathrm{~K} ）、 6969 （ T=288 KT=288 \mathrm{~K} ）、 6565 （ T=293 KT=293 \mathrm{~K} ）、 6262 （ T=298 KT=298 \mathrm{~K} ）、 5959 （ T=303 KT=303 \mathrm{~K} ）、 5656 （ T=308 KT=308 \mathrm{~K} ）、 5454 （ T=313 KT=313 \mathrm{~K} ）、 5050 （ T=323 KT=323 \mathrm{~K} ）和 4747 （ T=333 KT=333 \mathrm{~K} ）（见辅助信息中包含的学生书面说明）。（ii）其次， λNa+\lambda^{\mathrm{Na}+} 的值近似为无限稀释溶液中的值 λ∞Na+\lambda_{\infty}{ }^{\mathrm{Na}+} 。Benson和Gordon²³报告的实验数据通过线性插值法计算了 λ∞Na+\lambda_{\infty}{ }^{\mathrm{Na}+} 值： 34.734.7 （ T=284 KT=284 \mathrm{~K} ）、 39.339.3 （ T=288 KT=288 \mathrm{~K} ）、 44.944.9 （ T=293 KT=293 \mathrm{~K} ）、 50.650.6 （ T=298 KT=298 \mathrm{~K} ）、 56.356.3 （ T=303 KT=303 \mathrm{~K} ）、 62.062.0 （ T=308 KT=308 \mathrm{~K} ）、 67.767.7 （ T=313 KT=313 \mathrm{~K} ）、 79.079.0 （ T=323 KT=323 \mathrm{~K} ）和 90.390.3 （ T=333 KT=333 \mathrm{~K} ）（见辅助信息中包含的学生书面说明）。

5 材料与方法

电泳级SDS由Sigma提供并直接使用。溶液用去离子水（10 MΩ cm）配制，该水先前已在配备0.22 μm孔径滤器的商用Millipore Milli-Q系统（MQ水）中过滤。为了进行电导率测量，配制了五种浓度低于0.20% w/v（0.01、0.05、0.09、0.12和0.18% w/v）和五种浓度高于0.30% w/v（0.30、0.40、0.50、0.60和0.70% w/v）的SDS溶液。

将装有不同浓度SDS溶液的玻璃瓶放入配有Julabo EM恒温器的恒温水槽中。温度调节精度为0.2°C。为了测定溶液的电导率，使用了型号为162 A的数字台式电导率仪。该数字电导率仪先前已用两种氯化钠标准溶液进行校准：692 ppm（1413 μS cm⁻¹）和7230 ppm（12.9 mS cm⁻¹），以确定电池常数。

6 危险性

制备SDS固体制剂溶液时必须特别小心，因为它可能引起呼吸道和皮肤过敏反应。本实验没有其他重大危险。

7 结果

对SDS溶液在不同温度下进行了电导率测量。在标准实验室实验中获得的结果如图1所示。对于每个温度，随着SDS浓度的变化，观察到电导率的拐点。这些结果与Goddard和Benson观察到的结果高度一致¹⁷。

对每个温度下拐点前后的电导率数据进行了线性回归分析。在所有情况下，线性拟合都是准确的，并且在所使用的浓度范围内未观察到显著的非线性偏差。CMC值通过“Williams方法”在每个温度下确定，该方法包括求解相应的线性方程组。另外，也可以采用“Phillips方法”，该方法通过一个倒高斯函数近似电导率-浓度曲线的二阶导数。在该方法中，CMC将与倒高斯函数的最小值重合。然而，Mosquera及其同事²⁴已表明，对于SDS，Phillips方法与Williams方法得到的结果相同。表1中所示的结果对应于Williams方法。

CMC在25°C下的值为8.2 mM，与使用相同技术获得的文献值⁵˒¹⁷˒²⁵吻合良好。不确定度 Δ(CMC)=±0.1 mM\Delta(\mathrm{CMC})= \pm 0.1 \mathrm{~mM} 是通过对同一组样品进行五次独立测量取平均值计算得出的，与先前报道的值⁴相当。图2显示了 ln⁡CMC\ln \mathrm{CMC} 随温度的变化，在20至25°C之间观察到一个最小值。对于SDS，不同作者通过电导法¹⁷、声学法²⁶和紫外-可见光谱法²⁷均报道了类似最小值的存在。图2显示了采用Kim和Lim¹⁶推荐的 ln⁡CMC=A+BT+C/T\ln \mathrm{CMC}=A+B T+C/T 形式的拟合结果。在进行拟合时应特别注意使用绝对温度标度。通过设定 A=−30A=-30 、 B=0.0044 K−1B=0.0044 \mathrm{~K}^{-1} 和 C=3817 KC=3817 \mathrm{~K} ，获得了 R2=0.9998R^2=0.9998 的拟合。因此，上述方程适用于计算 ∂ln⁡CMC/∂T\partial \ln \mathrm{CMC}/\partial T 。

在每个温度下， α\alpha 通过方程12计算。在整个温度范围内，观察到 α\alpha 随温度呈线性依赖关系，斜率为 0.0013 K−10.0013 \mathrm{~K}^{-1} （数据未显示）。此时，CMC、 α\alpha 及其温度依赖性可直接用于分别使用方程5和6计算 ΔmicHˉ∘\Delta_{\mathrm{mic}} \bar{H}^{\circ} 和 ΔmicSˉ∘\Delta_{\mathrm{mic}} \bar{S}^{\circ} 。在不同温度下获得的 ΔmicGˉ∘\Delta_{\mathrm{mic}} \bar{G}^{\circ} 、 ΔmicHˉ∘\Delta_{\mathrm{mic}} \bar{H}^{\circ} 和 ΔmicSˉ∘\Delta_{\mathrm{mic}} \bar{S}^{\circ} 结果列于表1中，并描绘在图3中。请注意， ΔmicGˉ∘(T=298 K)=−21.2 kJ mol−1\Delta_{\mathrm{mic}} \bar{G}^{\circ}(T=298 \mathrm{~K})=-21.2 \mathrm{~kJ} \mathrm{~mol}^{-1} 的值与Benrraou等人¹³获得的值相同，也接近Aniansson等人¹⁹报道的值（ −22.6 kJ mol−1-22.6 \mathrm{~kJ} \mathrm{~mol}^{-1} ）。 ΔmicHˉ∘\Delta_{\mathrm{mic}} \bar{H}^{\circ} 值略低于文献中发现的量热值¹⁴˒²⁸。有趣的是， ΔmicGˉ∘\Delta_{\mathrm{mic}} \bar{G}^{\circ} 在所有温度下保持负值且相对恒定，证实当浓度达到CMC值时，胶束形成是自发发生的。此外， ΔmicGˉ∘\Delta_{\mathrm{mic}} \bar{G}^{\circ} 值的恒定性揭示了在所有温度下 ΔmicHˉ∘\Delta_{\mathrm{mic}} \bar{H}^{\circ} 和 TΔmicSˉ∘T\Delta_{\mathrm{mic}} \bar{S}^{\circ} 之间的抵消效应。

表1. 不同温度下SDS胶束化的CMC、 α\alpha 和热力学参数

T/K CMC/mM α\alpha ΔmicGˉ∘/(kJmol−1)\Delta_{\mathrm{mic}} \bar{G}^{\circ} /\left(\mathrm{kJ} \mathrm{mol}^{-1}\right) ΔmicHˉ∘/(kJmol−1)\Delta_{\mathrm{mic}} \bar{H}^{\circ} /\left(\mathrm{kJ} \mathrm{mol}^{-1}\right) ΔmicSˉ∘/(JK−1 mol−1)\Delta_{\mathrm{mic}} \bar{S}^{\circ} /\left(\mathrm{J} \mathrm{K}^{-1} \mathrm{~mol}^{-1}\right)
284 8.4 0.19 -20.4 -0.6 70
288 8.2 0.20 -20.7 -2.1 65
293 8.0 0.21 -21.1 -4.1 58
298 8.2 0.22 -21.2 -6.2 50
303 8.2 0.22 -21.6 -8.3 44
308 8.4 0.23 -21.7 -10.3 37
313 8.7 0.24 -21.8 -12.5 30
323 9.2 0.25 -22.1 -16.7 17
333 9.2 0.26 -22.3 -21.0 4

图1. 在11°C (•)、15°C (◊)、20°C (△)、25°C (▲)、30°C (●)、35°C (○)、40°C (□)、50°C (■) 和60°C (×) 下记录的电导率 ( κ\kappa ) 随SDS浓度的变化。

图2. SDS的 ln⁡CMC\ln \mathrm{CMC} 随温度的变化。实线表示 ln⁡CMC=A+BT+C/T\ln \mathrm{CMC}=A+B T+C/T 形式的函数。误差棒是根据对同一组样品进行五次独立测量取平均值计算得出的。

图3. 热力学参数 ΔmicGˉ∘\Delta_{\mathrm{mic}} \bar{G}^{\circ} 、 ΔmicHˉ∘\Delta_{\mathrm{mic}} \bar{H}^{\circ} 和 TΔmicSˉ∘T\Delta_{\mathrm{mic}} \bar{S}^{\circ} 随温度的变化。

8 讨论

从这些实验中获得的热力学信息可能有助于激发学生对原始数据进行批判性评估的兴趣。在这种背景下，实验室教师可能会提出几个相关问题：

作为对这些问题的可能回答，可以考虑以下物理论点。与溶液中的单体状状态相比，聚集成胶束状态的表面活性剂表现出更有序的结构。因此，人们可能会倾向于得出胶束化应该涉及系统熵减少的结论。然而，这种推理与实验证据不符，实验证据表明在低温下 ΔmicSˉ∘\Delta_{\mathrm{mic}} \bar{S}^{\circ} 为正。这种表面上的悖论可以通过考虑仅凭表面活性剂的自由度不能提供完整图像，并且表面活性剂结构的重组涉及伴随的溶剂结构变化来解释。事实上，围绕胶束的水分子与溶剂化单个SDS单体的水分子相比，其组织程度较低。这种效应会导致一个正的熵贡献，该贡献超过了由于SDS自由度损失而引起的熵减少。

随着温度升高，表面活性剂分子的溶剂化结构预计会逐渐减弱。Evans和Wightman¹⁸表明，对于十四烷基三甲基溴化铵，溶剂化效应在高于116°C的温度下变得可以忽略不计。因此，当温度升高时，由于水分子在胶束化过程中的贡献减少，预计 ΔmicSˉ∘\Delta_{\mathrm{mic}} \bar{S}^{\circ} 会下降。

ΔmicHˉ∘\Delta_{\mathrm{mic}} \bar{H}^{\circ} 和 ΔmicSˉ∘\Delta_{\mathrm{mic}} \bar{S}^{\circ} 随温度显示出大的线性变化。然而，这些变化相互抵消，导致 ΔmicGˉ∘\Delta_{\mathrm{mic}} \bar{G}^{\circ} 的值在整个研究温度范围内几乎不变。这种现象在文献中被称为“补偿现象”。从这个热力学观点来看，SDS胶束化在低温下被认为是熵驱动过程，在高温下被认为是焓驱动过程。

9 结论

我们提出了一项新的实验室实验，通过胶束系统引入基本热力学概念。数据的合理化可以置于“闭合缔合模型”的框架内，该模型建立了表面活性剂****单体和胶束状态之间的平衡。我们已经表明，在不同温度下进行的表面活性剂溶液电导率测量是评估理论方法中两个关键要素——CMC和胶束电离度 α\alpha ——的便捷途径。该实验技术代表了一种无害、简单、稳健且可重现的实验室实验，可以在本科生实验室课程中进行。对描述胶束化过程的不同热力学量的温度趋势的简单考虑，可用于进行有趣的讨论，以合理化控制溶液中这种聚集过程的基本机制。